Catalogue Entry: NATP00220

^[1] {Se}{p}t 1664.

^[2]

^[3]

^[4]

^[5]

^[6]

^[7]

^[8]

^[9]

^[10]

^[11]

^[12]

^[13]

^[14]

^[15]

^[16]

^[17]

^[18]

^[19]

^[20]

^[21]

^[22]

^[23]

^[24]

^[25]

^[26]

^[27]
{illeg} $2\mathrm{x}+\frac{1}{3}\mathrm{x}\mathrm{x}={\mathrm{gd}}^2$. $\mathrm{x}\mathrm{x}+4\mathrm{x}+1={\mathrm{ag}}^2$.

^[28] $\begin{array}{l}\underset{\_}{36}\hfill \\ 2025\\ \underset{\_}{162\phantom{0}}\\ \phantom{0}405\end{array}$

$\begin{array}{l}\underset{\_}{29376}\\ \underset{\_}{162}\\ \underset{\_}{29376}\\ \phantom{0}\underset{\_}{7776}\\ \phantom{0}\underset{\_}{729\phantom{0}}\\ \phantom{00}\underset{\_}{486}\end{array}$ $\underset{\text{'}}{\mathrm{a}}\_\_\_\_\_\_\_\_\_\_\_\_\underset{\text{'}}{\mathrm{b}}\_\_\_\_\_\underset{\text{'}}{\mathrm{c}}$ $\begin{array}{l}\underset{\_}{32076\times 25\mathrm{d}\mathrm{d}}=801900\mathrm{d}\mathrm{d}\\ 160380\\ \underset{\_}{64152}\end{array}$ $\begin{array}{l}729\\ \phantom{0}7290\end{array}$ $\begin{array}{l}134\\ \phantom{0}537\\ \phantom{0}\underset{\_}{486}\\ \phantom{00}5184\\ \phantom{00}486\\ \phantom{000}324\end{array}$ $\begin{array}{l}\phantom{0}1296\\ \phantom{0}648\\ 962\end{array}\}=\begin{array}{c}\underset{\_}{104976\times 9}\\ 944784\end{array}$ $\begin{array}{c}\phantom{0}900\\ \phantom{0}36\\ 1800\end{array}$ $\begin{array}{l}\phantom{0}405\\ \underset{\_}{162\phantom{0}}\\ \underset{\_}{2025\times 25\mathrm{d}\mathrm{d}}=50625\\ 10125\\ 4050\end{array}$ $\begin{array}{l}Q:\underset{\_}{324}=104976\\ \phantom{0}1296\\ \phantom{0}648\\ 972\end{array}$ $\begin{array}{l}\phantom{0}216\\ \underset{\_}{106}\\ \phantom{000}6\end{array}$ $\begin{array}{cc}36& \\ & \begin{array}{r}\phantom{0}216\\ \underset{\_}{106}\phantom{0}\end{array}\\ & 1276\\ & 11484\end{array}$ $\begin{array}{rr}9\times 25\times & 36\\ 3& 24\\ 16& 20\\ \underset{\_}{64}& \underset{\_}{8}\hfill \\ 81& 00\\ \underset{\_}{18}& \underset{\_}{00}\hfill \\ 99\end{array}$

$\begin{array}{r}36\times 324\\ \phantom{0}1944\\ \underset{\_}{\phantom{0}972\phantom{0}}\\ 11664\end{array}$ $\mathrm{x}+\frac{\mathrm{r}}{\mathrm{q}}\mathrm{x}\mathrm{x}=9$. $\frac{\mathrm{r}}{2}+\frac{\mathrm{r}\mathrm{x}\mathrm{q}}{\mathrm{q}}=2$ {illeg}$\mathrm{x}=2\mathrm{x}-\frac{\mathrm{r}\mathrm{x}}{2}$ . $\frac{\mathrm{r}\mathrm{x}}{2}+2\mathrm{x}=9$.
$\mathrm{x}=3$. $\mathrm{r}\mathrm{x}=6$ $\mathrm{r}=2$ $\mathrm{r}\mathrm{x}+4\mathrm{x}=18$ $-\frac{\mathrm{q}\mathrm{r}}{2}+2\mathrm{q}=\mathrm{r}\mathrm{x}$

$2\mathrm{q}-\frac{\mathrm{q}\mathrm{r}}{2}+4\mathrm{x}=18$ $\frac{\mathrm{q}\mathrm{r}}{2}+\frac{72}{\mathrm{r}+4}-18=0$

^[29] $\mathrm{c}\mathrm{c}=52\mathrm{c}-117$. $\begin{array}{r}\mathrm{c}=\mathrm{2\; 6}-\sqrt{156}\phantom{(0}\\ \underset{\_}{520}\phantom{(0}\\ 559(2\\ 4\\ 1\phantom{00(0}\end{array}$ $\mathrm{c}\mathrm{c}=80\mathrm{c}-180$

^[30] $\begin{array}{c}& \begin{array}{l}1600\\ 14\\ 1420(3\\ \phantom{00}20\end{array}\\ \phantom{0}\\ \begin{array}{ccc}13& .& \mathrm{}\\ 14& .& 192\\ 15& .& 225\\ 16& .& 5\\ 17& .& 289\\ 18& .& 324\\ 19& .& 361\\ 20& .& 400\end{array}\end{array}$

^[31] {illeg}

^[32]

${\mathrm{x}}^3+{\mathrm{y}}^3-\mathrm{a}\mathrm{x}\mathrm{y}=0$. $\mathrm{v}=\frac{3\mathrm{x}\mathrm{x}\mathrm{y}-\mathrm{a}\mathrm{y}\mathrm{y}}{\mathrm{a}\mathrm{x}-3\mathrm{y}\mathrm{y}}$ $\mathrm{x}+\frac{3\mathrm{x}\mathrm{x}{\mathrm{y}}^2-\mathrm{a}\mathrm{y}\mathrm{y}\mathrm{z}}{\sqrt{\begin{array}{c}9{\mathrm{x}}^4\mathrm{y}\mathrm{y}-6\mathrm{a}\mathrm{x}\mathrm{x}{\mathrm{y}}^3\\ +\mathrm{a}\mathrm{a}{\mathrm{y}}^4+\mathrm{a}\mathrm{a}\mathrm{x}\mathrm{x}\mathrm{y}\mathrm{y}\\ -6{\mathrm{a}}^3\mathrm{x}\mathrm{y}\mathrm{y}+9{\mathrm{a}}^4{\mathrm{y}}^4\\ \end{array}}}$ for x. $\mathrm{x}+\frac{3\mathrm{z}\mathrm{x}\mathrm{x}-\mathrm{a}\mathrm{z}\mathrm{y}}{\sqrt{\begin{array}{c}9{\mathrm{x}}^4-6\mathrm{a}\mathrm{y}\mathrm{x}\mathrm{x}+10\mathrm{a}\mathrm{a}\mathrm{y}\mathrm{y}\\ +\mathrm{a}\mathrm{a}\mathrm{x}\mathrm{x}-6{\mathrm{a}}^3\mathrm{x}\end{array}}}$ for x . $\mathrm{y}\frac{+3\mathrm{y}\mathrm{y}\mathrm{z}-\mathrm{a}\mathrm{z}\mathrm{x}}{\sqrt{\begin{array}{c}9{\mathrm{x}}^4-6\mathrm{a}\mathrm{y}{\mathrm{x}}^2+10{\mathrm{a}}^2{\mathrm{y}}^2\\ +\mathrm{a}\mathrm{a}{\mathrm{x}}^2-6{\mathrm{a}}^3\mathrm{x}\end{array}}}$ for y

$\mathrm{a}\mathrm{b}=\mathrm{a}=2\mathrm{a}\mathrm{d}$ $\mathrm{a}\mathrm{d}=\frac{\sqrt{3\mathrm{a}\mathrm{a}}}{4}$

^[33]

{illeg}$=\mathrm{x}$. $\mathrm{ce}=\mathrm{y}$. $\mathrm{af}=\mathrm{q}$. {illeg}$\mathrm{x}-\mathrm{x}\mathrm{x}=\mathrm{y}\mathrm{y}$. $\mathrm{ed}=\mathrm{z}$. $\mathrm{ed}=\mathrm{s}$. {illeg}$\mathrm{c}=\mathrm{q}-\mathrm{x}$. ${\mathrm{eb}}^2=\mathrm{q}\mathrm{q}$. $\mathrm{eb}=\mathrm{q}$. {illeg}$:2\mathrm{q}\mathrm{x}-\mathrm{x}\mathrm{x}:\mathrm{z}\mathrm{z}:$ ${\mathrm{eh}}^2$. $\mathrm{eh}=\sqrt{\frac{2\mathrm{q}\mathrm{x}\mathrm{z}\mathrm{z}-\mathrm{x}\mathrm{x}\mathrm{z}\mathrm{z}}{\mathrm{q}\mathrm{q}}}$ {illeg}= $\sqrt{2\mathrm{q}\mathrm{x}-\mathrm{x}\mathrm{x}}-\frac{\mathrm{z}}{\mathrm{q}}\sqrt{\phantom{00000}\mathrm{x}\mathrm{x}}$ {illeg} $=2\mathrm{q}\mathrm{x}-\mathrm{x}\mathrm{x}+\frac{2\mathrm{z}\mathrm{z}\mathrm{q}\mathrm{x}-\phantom{000}}{\mathrm{q}\mathrm{q}}$ {illeg}$-4\mathrm{z}\mathrm{x}+\frac{2\mathrm{z}\mathrm{x}\mathrm{x}}{\mathrm{q}}$ {illeg}$=\frac{\mathrm{q}\mathrm{z}-\mathrm{x}\mathrm{z}}{\mathrm{q}}$ {illeg}$-\frac{\mathrm{z}\mathrm{x}}{\mathrm{q}}$

^[34]

^[35]

^[36] $\begin{array}{cccc}& \mathrm{d}\mathrm{x}\mathrm{q}\mathrm{y}& +& 2\mathrm{f}\mathrm{x}\mathrm{y}\mathrm{y}\\ -& 2\mathrm{p}\mathrm{f}\mathrm{x}\mathrm{y}& -& \mathrm{b}\mathrm{y}\mathrm{x}\\ -& 2\mathrm{a}\mathrm{y}\mathrm{y}\mathrm{x}& -& \frac{\mathrm{d}\mathrm{e}\mathrm{x}\mathrm{y}-\mathrm{d}\mathrm{d}\mathrm{y}\mathrm{y}\mathrm{y}}{\mathrm{f}}\end{array}$

^[37] {illeg} $\begin{array}{ccccc}\mathrm{x}\mathrm{y}& +& \mathrm{a}\mathrm{y}& =& 0\\ \mathrm{a}\mathrm{x}& +& \mathrm{y}\mathrm{y}\end{array}$

$\mathrm{ed}=\mathrm{v}$. $\mathrm{cd}=\mathrm{x}$. $\mathrm{ac}=\mathrm{y}$. $\mathrm{ab}=\mathrm{s}$. {illeg}$=\mathrm{z}$. $\mathrm{eg}=\mathrm{\xi }$. $0=\mathrm{y}\mathrm{y}-2\mathrm{x}\mathrm{y}+\mathrm{a}\mathrm{x}-{\mathrm{x}}^2$ $\mathrm{y}=$ $\stackrel{\cup }{O}\sqrt{2\mathrm{x}\mathrm{x}-\mathrm{a}\mathrm{x}}=\mathrm{ac}$ $\mathrm{y}\mathrm{y}=\begin{array}{c}2\mathrm{x}\mathrm{x}\\ -\mathrm{a}\mathrm{x}\end{array}\stackrel{\cup }{O}2\sqrt{2{\mathrm{x}}^4-\mathrm{a}{\mathrm{x}}^3}$. ${\mathrm{eg}}^2=\begin{array}{c}3{\mathrm{x}}^2-60\mathrm{x}-\mathrm{a}\mathrm{x}+\mathrm{a}\mathrm{o}\\ \stackrel{\cup }{O}\sqrt{2{\mathrm{x}}^4-\mathrm{a}{\mathrm{x}}^3}\end{array}$. ${\mathrm{eg}}^2=\begin{array}{c}3{\mathrm{z}}^2\\ -\mathrm{a}\mathrm{z}\end{array}\stackrel{\cup }{O}\sqrt{2{\mathrm{z}}^4-\mathrm{a}{\mathrm{z}}^3}$ $\mathrm{y}\mathrm{y}-2\mathrm{x}\mathrm{y}+\mathrm{a}\mathrm{x}-\mathrm{x}\mathrm{x}=0$ $\frac{-2\mathrm{y}\mathrm{y}+\mathrm{a}\mathrm{y}-2\mathrm{x}\mathrm{y}}{-2\mathrm{y}+2\mathrm{x}}+\mathrm{x}=\mathrm{v}$ $\mathrm{x}+\mathrm{y}+\frac{\mathrm{a}\mathrm{y}}{2\mathrm{x}-2\mathrm{y}}=\mathrm{v}$ $8{\mathrm{x}}^4-4\mathrm{a}{\mathrm{x}}^3+4\mathrm{a}{\mathrm{z}}^3-8{\mathrm{z}}^4$ $\begin{array}{r}{\mathrm{x}}^3+4\mathrm{x}\mathrm{x}\mathrm{z}+4\mathrm{x}\mathrm{z}\mathrm{z}+4{\mathrm{z}}^3\\ -2\mathrm{x}\mathrm{x}\mathrm{a}-2\mathrm{a}\mathrm{x}\mathrm{z}-2\mathrm{a}{\mathrm{z}}^2\end{array}$ $\begin{array}{ccc}\sqrt{2\mathrm{x}\mathrm{x}-\mathrm{a}\mathrm{x}}& -& 2\mathrm{z}\sqrt{2\mathrm{z}\mathrm{z}-\mathrm{a}\mathrm{z}}\\ & +& 2\mathrm{z}\sqrt{2\mathrm{x}\mathrm{x}-\mathrm{a}\mathrm{x}}\end{array}$

$\mathrm{ab}=\mathrm{a}$. $\mathrm{bd}:\mathrm{be}\colon\colon \mathrm{b}:\mathrm{c}$. $\frac{\mathrm{c}\mathrm{x}}{\mathrm{b}}=\mathrm{be}$ . $\frac{\mathrm{c}\mathrm{ϩ}}{\mathrm{b}}=\mathrm{eh}$. ${\mathrm{fe}}^2==\frac{\mathrm{c}\mathrm{c}\mathrm{ϩ}\mathrm{ϩ}-\mathrm{b}\mathrm{b}\mathrm{ϩ}\mathrm{ϩ}}{\mathrm{b}\mathrm{b}}$ $\mathrm{fe}=\frac{\mathrm{c}\mathrm{x}-\mathrm{b}\mathrm{z}}{\mathrm{b}}=\frac{\mathrm{ϩ}\sqrt{\mathrm{c}\mathrm{c}-\mathrm{b}\mathrm{b}}}{\mathrm{b}}$ $\frac{\mathrm{b}\mathrm{z}+\mathrm{ϩ}\sqrt{\mathrm{c}\mathrm{c}-\mathrm{b}\mathrm{b}}}{\mathrm{c}}=\mathrm{x}$ $\mathrm{ed}=\frac{\mathrm{x}\sqrt{\mathrm{c}\mathrm{c}-\mathrm{b}\mathrm{b}}}{\mathrm{b}}$ $\mathrm{ed}=\frac{\mathrm{ϩ}\mathrm{c}\mathrm{c}-\mathrm{ϩ}\mathrm{b}\mathrm{b}+\mathrm{b}\mathrm{z}\sqrt{\mathrm{c}\mathrm{c}-\mathrm{b}\mathrm{b}}}{\mathrm{b}\mathrm{c}}$ $\mathrm{eh}=\frac{-\mathrm{ϩ}\mathrm{b}+\mathrm{z}\sqrt{\mathrm{c}\mathrm{c}-\mathrm{b}\mathrm{b}}-\mathrm{c}\mathrm{a}}{\mathrm{b}}$

^[38]

^[39] $\mathrm{ϩ}\sqrt{\mathrm{e}\mathrm{c}-\mathrm{d}\mathrm{d}}=\mathrm{e}\mathrm{x}$ .

^[40] {illeg}$\begin{array}{c}\phantom{0}\\ \phantom{0}\end{array}+4{\mathrm{d}}^3{\mathrm{\varrho }}^3\mathrm{ϩ}\sqrt{\mathrm{e}\mathrm{e}-\mathrm{d}\mathrm{d}}+$

^[41] {illeg}$\begin{array}{c}\phantom{0}\\ \phantom{0}\\ \phantom{0}\end{array}{\mathrm{\varrho }}^5+5{\mathrm{d}}^4{\mathrm{\varrho }}^4\mathrm{ϩ}\sqrt{\mathrm{e}\mathrm{e}-\mathrm{d}\mathrm{d}}$

^[42] {illeg}$\begin{array}{c}\phantom{0}\\ \phantom{0}\end{array}-\mathrm{d}\mathrm{ϩ}+\mathrm{\varrho }\sqrt{\mathrm{e}\mathrm{e}-\mathrm{d}\mathrm{d}}=\mathrm{e}\mathrm{y}$.

^[43] $\mathrm{\varrho }\begin{array}{l}-2\mathrm{d}\mathrm{d}\mathrm{\varrho }\mathrm{ϩ}\\ +\mathrm{e}\mathrm{e}\mathrm{\varrho }\mathrm{ϩ}\end{array}\begin{array}{l}\phantom{0}\\ +\mathrm{c}\mathrm{e}\mathrm{ϩ}\sqrt{\mathrm{e}\mathrm{e}-\mathrm{d}\mathrm{d}}\\ \end{array}=\mathrm{e}\mathrm{e}\mathrm{x}\mathrm{y}$.

^[44] $\begin{array}{c}\mathrm{d}{\mathrm{ϩ}}^3\\ {\mathrm{ϩ}}^3\end{array}+2\mathrm{c}\mathrm{e}\mathrm{\varrho }\mathrm{ϩ}\sqrt{\mathrm{e}\mathrm{e}-\mathrm{d}\mathrm{d}}\begin{array}{ll}+& 2\mathrm{d}\mathrm{e}\mathrm{e}\mathrm{\varrho }\mathrm{\varrho }\mathrm{ϩ}\\ -& 3{\mathrm{d}}^3\mathrm{\varrho }\mathrm{\varrho }\mathrm{ϩ}\end{array}\}={\mathrm{e}}^3\mathrm{x}\mathrm{x}\mathrm{y}$

^[45] {illeg} $\mathrm{x}+\mathrm{a}\mathrm{x}+\mathrm{b}\mathrm{b}=0$ . {illeg} $+\frac{\mathrm{a}\mathrm{a}}{0}+\mathrm{b}\mathrm{b}$

^[46] $\mathrm{ac}=\mathrm{d}$. {illeg}$=\mathrm{a}$. $\mathrm{ad}=\mathrm{b}$. $\mathrm{ed}=\mathrm{c}$. $\frac{\mathrm{a}\mathrm{a}}{\mathrm{b}}=\mathrm{ab}$. $\mathrm{ae}=\mathrm{e}$ {$\frac{\mathrm{a}\mathrm{e}}{\mathrm{b}}=\mathrm{eb}$.} $\mathrm{bc}=\frac{\mathrm{d}\mathrm{b}-\mathrm{a}\mathrm{a}}{\mathrm{b}}$ {illeg} ${\mathrm{c}}^2=$ $\mathrm{c}\mathrm{c}$ . $\frac{\mathrm{d}\mathrm{d}\mathrm{b}\mathrm{b}-2\mathrm{a}\mathrm{a}\mathrm{b}\mathrm{d}+{\mathrm{a}}^4+\mathrm{a}\mathrm{a}\mathrm{c}\mathrm{c}}{\mathrm{b}\mathrm{b}}=\mathrm{e}\mathrm{e}$.

^[47]
{illeg}$\mathrm{d}=\mathrm{a}$. $\mathrm{pg}=\mathrm{b}$. $\mathrm{pd}=\mathrm{g}$ $\frac{\mathrm{e}\mathrm{a}}{\mathrm{d}}=\mathrm{dh}$ . $\frac{\mathrm{f}\mathrm{a}}{\mathrm{d}}=\mathrm{gh}$ . $\mathrm{h}=\frac{\mathrm{b}\mathrm{d}-\mathrm{f}\mathrm{a}}{\mathrm{d}}$ . {illeg} $\mathrm{b}\mathrm{d}\mathrm{d}-2\mathrm{b}\mathrm{d}\mathrm{f}\mathrm{a}+\mathrm{a}\mathrm{a}\mathrm{f}\mathrm{f}+\mathrm{e}\mathrm{e}\mathrm{a}\mathrm{a}=\mathrm{b}\mathrm{b}\mathrm{g}\mathrm{g}$ {illeg} $\begin{array}{c}\mathrm{a}\mathrm{e}\mathrm{e}\\ \mathrm{a}\mathrm{a}\mathrm{d}\mathrm{d}\end{array}=2\mathrm{b}\mathrm{d}\mathrm{a}\sqrt{\mathrm{e}\mathrm{e}-\mathrm{d}\mathrm{d}}+\mathrm{b}\mathrm{b}\mathrm{g}\mathrm{g}-\mathrm{b}\mathrm{b}\mathrm{d}\mathrm{d}$ . {illeg} $\mathrm{a}=\frac{\mathrm{b}\mathrm{d}\sqrt{\mathrm{e}\mathrm{e}-\mathrm{d}\mathrm{d}}}{2\mathrm{e}\mathrm{e}-\mathrm{d}\mathrm{d}}\stackrel{\cup }{O}\sqrt{\frac{-\mathrm{b}\mathrm{b}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{e}+2\mathrm{b}\mathrm{b}\mathrm{g}\mathrm{g}\mathrm{e}\mathrm{e}-\mathrm{b}\mathrm{b}\mathrm{g}\mathrm{g}\mathrm{d}\mathrm{d}}{4{\mathrm{e}}^4-4\mathrm{e}\mathrm{e}\mathrm{d}\mathrm{d}+{\mathrm{d}}^4}}$

^[48]

^[49]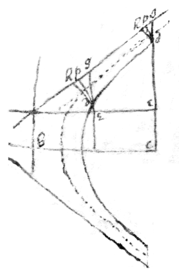

^[50]

^[51]

^[52]

^[53]

^[54]

^[55] September 1664

^[56]

^[57]

^[58]

^[59] $\frac{\mathrm{d}\mathrm{\varrho }+\mathrm{s}\mathrm{ϩ}}{\mathrm{e}}=\mathrm{x}$. $\frac{\mathrm{t}\mathrm{\varrho }-\mathrm{v}\mathrm{ϩ}+\mathrm{c}\mathrm{e}}{\mathrm{e}}=$ y

^[60]

^[61]

$\mathrm{d}\mathrm{g}-\mathrm{e}\mathrm{g}-\mathrm{e}\sqrt{\mathrm{d}\mathrm{d}-\mathrm{g}\mathrm{g}}+\mathrm{d}\sqrt{\mathrm{d}\mathrm{d}-\mathrm{g}\mathrm{g}}=0$. $\mathrm{g}=\sqrt{\mathrm{d}\mathrm{d}-\mathrm{g}\mathrm{g}}$. $\mathrm{d}\mathrm{d}=2\mathrm{g}\mathrm{g}$ or $\mathrm{d}=\mathrm{e}$ $\mathrm{a}\mathrm{g}-2\mathrm{c}\mathrm{g}-2\mathrm{c}\sqrt{\mathrm{d}\mathrm{d}-\mathrm{g}\mathrm{g}}=0$ $\frac{\mathrm{a}\mathrm{g}}{2\mathrm{g}+2\sqrt{\mathrm{d}\mathrm{d}-\mathrm{g}\mathrm{g}}}=\mathrm{c}$. ${\mathrm{g}}^3=-\mathrm{d}\mathrm{d}+\mathrm{g}\mathrm{g}\sqrt{\mathrm{d}\mathrm{d}-\mathrm{g}\mathrm{g}}$. $2\mathrm{g}\mathrm{g}=\mathrm{d}\mathrm{d}$. $-3\mathrm{c}\mathrm{c}\mathrm{d}\mathrm{d}\sqrt{\mathrm{d}\mathrm{d}-\mathrm{g}\mathrm{g}}=0=\mathrm{c}$. $3\mathrm{d}\mathrm{d}\mathrm{g}=3\mathrm{e}\mathrm{e}\sqrt{\mathrm{d}\mathrm{d}-\mathrm{g}\mathrm{g}}$ $\mathrm{d}=\mathrm{e}$. $-\mathrm{a}\mathrm{e}\mathrm{g}\mathrm{d}$ $\begin{array}{l}-6\mathrm{c}\mathrm{d}\mathrm{e}\sqrt{\mathrm{d}\mathrm{d}-\mathrm{g}\mathrm{g}}=\mathrm{a}\mathrm{d}\mathrm{e}\mathrm{g}=0\\ +\mathrm{a}\mathrm{d}\mathrm{d}\hfill \end{array}$ $-3\mathrm{d}\mathrm{d}\mathrm{c}\mathrm{c}\sqrt{\mathrm{d}\mathrm{d}-\mathrm{g}\mathrm{g}}-\mathrm{a}\mathrm{d}\mathrm{d}\mathrm{c}\mathrm{g}=0$ $9\mathrm{c}\mathrm{c}\mathrm{d}\mathrm{d}-9\mathrm{c}\mathrm{c}\mathrm{g}\mathrm{g}=\mathrm{a}\mathrm{a}\mathrm{g}\mathrm{g}$ . ${\mathrm{d}}^4\mathrm{g}\mathrm{g}=$ {${\mathrm{t}}^4-$}$\mathrm{g}\mathrm{g}{\mathrm{e}}^4$ $\begin{array}{llllll}& 36\mathrm{c}\mathrm{c}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{e}& -& 36\mathrm{c}\mathrm{c}\mathrm{g}\mathrm{g}\mathrm{e}\mathrm{e}& =& \mathrm{a}\mathrm{a}\mathrm{g}\mathrm{g}\mathrm{e}\mathrm{e}\\ +& \mathrm{a}\mathrm{a}{\mathrm{d}}^4& -& \mathrm{a}\mathrm{a}\mathrm{d}\mathrm{d}\mathrm{g}\mathrm{g}\\ -& 2\mathrm{c}\mathrm{e}\mathrm{a}{\mathrm{d}}^3\end{array}$ $-\mathrm{r}\sqrt{\mathrm{r}\mathrm{x}}-6\mathrm{x}\sqrt{\mathrm{r}\mathrm{x}}$ $\begin{array}{ccccccc}3\mathrm{r}\mathrm{x}& +& 8\mathrm{x}\mathrm{x}& +& \frac{16{\mathrm{x}}^3}{\mathrm{r}}& +& \frac{\mathrm{r}\mathrm{r}}{4}\\ & +& 4\mathrm{x}\mathrm{x}\end{array}$

^[62]

^[63]

^[64]

Ian 20^th 1664.

^[65]

^[66]

^[67] Noe motion is lost in reflection. For the circular motion being made by continuall reflection would decay.

^[68]

^[69] Def 3^d

^[70] {illeg}s Axiome 4^th.

^[71]

^[72] p Axiom 4^th.

^[73]
Of the seperation of body{s} after reflection

^[74] r axiome 3^d

^[75]

^[76]

^[77]

^[78] The center of motions determinacon & velocity

^[79] x axiom 14

^[80]

^[81]
Of endeavor from the center

^[82]

^[83]

^[84]

^[85]

^[86]

^[87] let this follow the 5^t axiom

^[88]

^[89] What force is required to beget or destroy equall velocity in unequall bodys

^[90]
What resistance in bodys

^[91] What force Indeavor & Pression is

^[92] What force or Motion is in equivelox bodys

^[93]
What velocity acquired or lost in equall bodys by unequall forces

^[94] What motion in bodys

^[95]
A generall Theorem of the proportion of velocity & motion of given body moving ☞ through given spaces in given times.

^[96] What force required to beget or destroy unequall celerity in equall bodys

^[97] Of hindering and helping motion

^[98] What celerity acquired or lost by equall forces in unequall bodys

^[99]
What velocity & motion gotten or lost by unequall forces in unequall bodys ☞ A Generall Theorem.

^[100] Of the {illeg} force in reflected bodys

^[101]

^[102]
Two bodys being uniformely moved in the same plaine their center of motion which describe a streight line

^[103]

{illeg} the {illeg} {as divers plaines}

^[104]
of the velocity of the center of motion 14

^[105] The 28^th & 30^th proposition done otherwise

^[106] Or thus

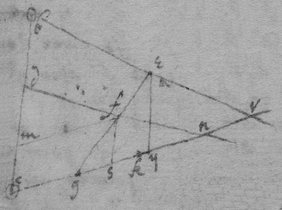
^[107]
The {illeg} of motion is {illeg} before after {illeg}

^[108]

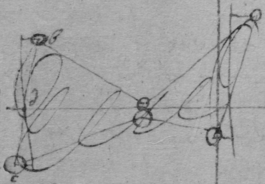
The center of motion in finite bodys hath the same velocity before & after reflection

^[109]
This ought to be proved by the 34^th & 35^t, & the 36^t by this concerning the impresse of $\left(\mathrm{g}\right)$ on $\left(\mathrm{qdp}\right)$

^[110]

Of the Advantage of force in divers positions to some center.

^[111]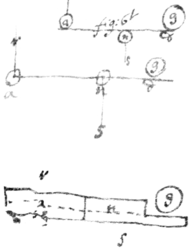

^[112]

^[113]

^[114]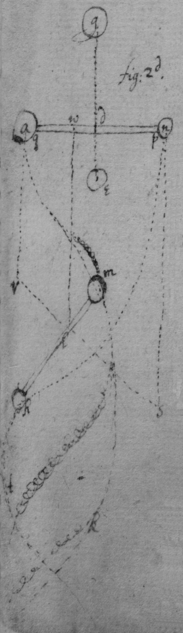
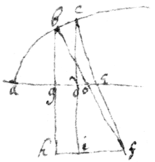
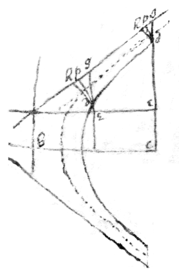
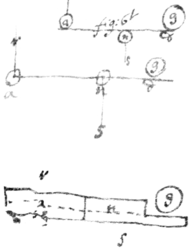