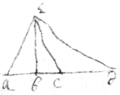Newton's Waste Book (Part 1)
{}{}
<ii(v)>{ } = {illeg} . to find the proportion of two irrationall rootes. to free the Numerato{r} or denom from {illeg}surde q{illeg} .
<iii(r)>To find a heavy bodys descent in any given time, & the proportion of the pressure of the rays by gravity to the force by which a body hath any given motion; by this figure  If the cilinders bc, df bee of glasse &c: the proportion of their strength is knowne by the proportion of the gravity of the circles
If the cilinders bc, df bee of glasse &c: the proportion of their strength is knowne by the proportion of the gravity of the circles  a, e &c in respect of the axis in.
a, e &c in respect of the axis in.
If a Staffe bee bended to find the crooked line which it resembles.
If the motion of a line is knowne to find the crooked line which that line toucheth continually.
If a stick
ab
revolves with even velocity about the center a haveing the weight c
 fastened {in} it by {the} string bc
, then shall the string bc
bee a tangent to the circle bde.
fastened {in} it by {the} string bc
, then shall the string bc
bee a tangent to the circle bde.
But it may be inquired what line the weight would describe were the stick with uneven velocity, or did the point b describe a Parabola or some other crooked line were the weight c in some other place as at the center { a } when the stick began to move.
If the ball
b
revolves about the center
n
the force by which it  endeavours from the center
n
would {beget} soe much motion in a body as there is in the time that the body
b
moves the length {of the} {semidiameter}
bn
. [as if
b
is moved with one degree of {motion} through e
bn
in {a} seacond of an {hower} than its force from the center {illeg} being continually like the force of gravity impressed upon the body during one second it will generate one degree of motion in that body.] Or the force from {n} in one revolution is to the force of the body motion as ∷
. Demonstration. If
. & the globe {b} from a to b {then} {ak}∷ force {or} pression of b upon fg {at} its reflecting ∶
force of b{'}s motion. therefore
fa
∷
force of the reflection in one round (viz: in b
, c
, d
, & a)
∶
force of
b
's motion. by the sa{me} pro{illeg} the Globe
b
were reflected by each side of a circumscribed polygon of 6, 8, 12, 100, 1000 sides {illeg} the force of all the reflections is to the force of the bodys as the sum of those sides {illeg} r{adius} of the circle about which they are circumscribed. And so if body were reflected by the sides of an equilaterall circumscribed polygon of an infinite number of sides {illeg} by {illeg} circle it selfe) the force of all the reflections are to the force of the bodys motion {as each} those sides ({illeg} the perimiter) to the radius.
endeavours from the center
n
would {beget} soe much motion in a body as there is in the time that the body
b
moves the length {of the} {semidiameter}
bn
. [as if
b
is moved with one degree of {motion} through e
bn
in {a} seacond of an {hower} than its force from the center {illeg} being continually like the force of gravity impressed upon the body during one second it will generate one degree of motion in that body.] Or the force from {n} in one revolution is to the force of the body motion as ∷
. Demonstration. If
. & the globe {b} from a to b {then} {ak}∷ force {or} pression of b upon fg {at} its reflecting ∶
force of b{'}s motion. therefore
fa
∷
force of the reflection in one round (viz: in b
, c
, d
, & a)
∶
force of
b
's motion. by the sa{me} pro{illeg} the Globe
b
were reflected by each side of a circumscribed polygon of 6, 8, 12, 100, 1000 sides {illeg} the force of all the reflections is to the force of the bodys as the sum of those sides {illeg} r{adius} of the circle about which they are circumscribed. And so if body were reflected by the sides of an equilaterall circumscribed polygon of an infinite number of sides {illeg} by {illeg} circle it selfe) the force of all the reflections are to the force of the bodys motion {as each} those sides ({illeg} the perimiter) to the radius.
If the body b moved in an Ellipsis then its force in each point (if its motion {in that point bee} g{illeg}) bee found by a tangent circle of equal crookednesse with that point of the Ellipsis.
If a body undulate in the circle
bd
all its undulations of any altitude are performed  in the {same} time with the same radius. Galileus.
in the {same} time with the same radius. Galileus.
As radius ab to radius ac ∷ so are the Squares of theire times in which they undulate.
If c circulate in the circle { cgef } , to whose diamiter { ce ,} being perpendicular then will the body b undulate in the same time that c circulate.
And those body circulate in the same time whose {illeg} {illeg} from the {illeg} to the center d are equall
And force of gravity to the force of { c } to its center d . {illeg} {illeg} {illeg} {illeg} the motion of things falling were they not hindered by the {illeg} may very {illeg} {illeg} force form d ∶ force from a.
<1v>[1] . . . . . [2] fig 2d. . + . . [3] . a {illeg}∶{illeg}f . Parab . ergo, .
[5] . . . . : ergo . & . Hyp: . . . .
[6] . . . , Ergo . . & . Ellipsis.
[7] . . . Ergo, . Hyperb.
[8]The invention of Figures for reflections. at right angles at the point reflecting ac the radius reflected to the focus b. ag the radius reflected from the focus b. aq a perpendicular to ed the tangent of the crooked line sought. . , or, . . , or, . , or . fig: 1st[9]. . Ergo, , or . & . ergo qg. . fig: 2d[10]. . Ergo, . &, . Ergo v. . fig 3d[11]. Ergo . Ergo, . & .
The invention of figures for refraction. b , & g the foci. ca the Radius refracted to b . qa the Radius refracted from b. bg the distance of the foci. qa the perpendicular to de the tangent of the crooked line sought qr, perpendiculars to the Radii cg, fb.
. . . . fig: 1st[12]. . , Ergo. . fig: 2d[13]. . ∷ , Ergo. e. fig 3d[14]. . . : Ergo . fig 4th[15]. . . : . fig 5t[16]. . . . . fig 6t. . . . d v .
. . . . .
. 2 . & . [17] . . m. =. . : therefore . . e
. .
{ef}. . . . . : & . . . . . . . [18] y. x. . . . . . . [19]
. . . . . . . . . . [20] [21]
[22] [23]  Make the line ac
to revolve about the point a
: on the end
c
let the nut
c
bee fastened so {as} to turne about its center. make & fastend another nut at the point b in the same manner. make the line
bc
to slide through those two nuts soe that the triangle
abc
will always be an isosceles. To the line
cb
fasten the line
rstv
at right angles. make the line
kg
with 2 nuts
e
&
d
at each end through which the lines
rs
&
tu
must slide to keepe the line
kg
perpendicular to
bc
, in the midst of
kg
fasten the nutt
m
so as it may turne about its center & that the line
ac
may slide through it then make that side of the line kg
which is next ab to be a file which must be very smooth at the point m
but must grow rougher towards the ends
d
&
e
. Then by turneing the line
ac
to & from
l
&
h
about its center & holding the file
kg
close to the plate
hmflab
, it shall file it into the shape of a Parabola.
Make the line ac
to revolve about the point a
: on the end
c
let the nut
c
bee fastened so {as} to turne about its center. make & fastend another nut at the point b in the same manner. make the line
bc
to slide through those two nuts soe that the triangle
abc
will always be an isosceles. To the line
cb
fasten the line
rstv
at right angles. make the line
kg
with 2 nuts
e
&
d
at each end through which the lines
rs
&
tu
must slide to keepe the line
kg
perpendicular to
bc
, in the midst of
kg
fasten the nutt
m
so as it may turne about its center & that the line
ac
may slide through it then make that side of the line kg
which is next ab to be a file which must be very smooth at the point m
but must grow rougher towards the ends
d
&
e
. Then by turneing the line
ac
to & from
l
&
h
about its center & holding the file
kg
close to the plate
hmflab
, it shall file it into the shape of a Parabola.
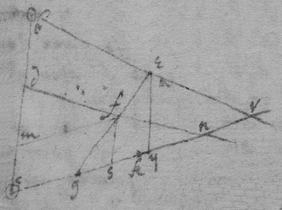
 To describe the Parabola by points. Make ; c
the vertex; a
the focus; . then with some radius as , describe the circle ge
: & take de & the point
e
shall bee in the parabola, also if from
e
to
g
, a streight line be drawne it shall touch the Parab: in e.
To describe the Parabola by points. Make ; c
the vertex; a
the focus; . then with some radius as , describe the circle ge
: & take de & the point
e
shall bee in the parabola, also if from
e
to
g
, a streight line be drawne it shall touch the Parab: in e.
Or thus, take , or :; & . &c:
Or thus, take , ; & ; &c.
Or thus take & raise me a perpendicular to ca, which shall intersect the parab, & circle ge in the same point.
 Or thus. make .
r. . with the Radius bc describe
bed
. the circle.
Or thus. make .
r. . with the Radius bc describe
bed
. the circle.
[24] Or thus take . Circle aen: . & produce mp indefinitely. Then take some point ad in the line an , & draw dg perpendic: to an that is soe that , then take , & f shall be a point in the parabola afr.
Banderon's addition to Ferrarius's Lexion Geographicum, the best for Geog. Ortelius Geogr. Lexicon.
Experiments about the resistance of things falling in water.
1. I filled to the top a wooden vessel 9 inches square within & 9 foot inches high within. And making balls of bees wax of several bignesses with pieces of Lead stuck in them to give them weight: three balls each of which weighed in the air grains & in the water grains, fell each of them in the water from the top to the bottom of the vessel in 15″ of time the motion of descent being (to {sence}) uniform almost from the top to the bottom. so then a globe equall to grains of water moving uniformly 9 foot inches in 15″ of time feels a resistance equal to grains of weight.
2. Two balls, each weighing in air grains in water 77 grains fell each of them the same height of 9 foot {dig.} in 4″ of time. And these experiments seemed sufficiently accurate.
Corol. Ergo the resistance is as the square of the velocity.
3. Two balls weighing each of them in air 245 grains, in water {almost} fell each the same height in ″. But these experiments were not so accurate as for{mers.}
The same two balls augmented with lead so as each of them to weigh in air in water
Three balls
Problems. 1 To find the axis, diameters, centers, asymptotes & vertices of lines
2 To compare their crookednesse with the crookednes of a given circle
3 To find the longest & shortest lines which can be drawn with in & perpendicular to the line & to find all such lines are perpendicular at both ends to the given crooked line
4 To find where their greatest or least crokedness.
5 To find the areas, the lengths, & centers of gravity of crooked lines when it may b{e}
[26] 6 If y (one undetermined quantity) moves perpendicularly to x (the other undetermin{ed} quantity. if . . . . Then having the proportion of v to {x}{s} to find y, or having the proportion of v to y to find x: when it may bee.
7 To reduce all kinds of equations, when it may bee
8 To find tangents to any crooked lines. Whither Geometricall or Mechanicall
9 To compare the superficies of one line with the area of another & to find the centers of gravity twixt two lines or sollids. 15
10 Haveing the position which x must beare to y (as if x is always in the same line, but y cutteth x at given angles. or if x & y wheeling about 2 poles describe the lines by theire intersection &c) to find theire position in respect of the line soe the equation expressing theire relation may bee as simple as may bee (as to find in what line x is & what angles it maketh with y; or to find the distance of the 2 poles & in what line they must be, soe that the relation twix{t} x & y may bee had in as simple termes as may bee).
11 Of the description of lines.
12 Reasonings of gravity & levity upon severall suppositions (as that the rays of gravity are parallel or verge towards a center; that they are reflected, refracted, or neith{er} by the weighty body &c.
13 Of the use of lines
< insertion from lower down f 4r >14. To find such lines whose areas length or centers of gravity may bee found.
15. To compare the areas, lengths, gravity of lines when it may bee. & to find such lines whose lengths, areas may be comp{illeg}
16. To doe the same to sollids in respect of theire areas, content, gravity &c which was done to lines in respect of their lengths, areas, & gravity.
17. Of lines which lye not in the same plane as those made by the intersection of a cone & {sphæreides}.
18. Two equations given to know whither they expresse the same line or not.
19. Of the proportion which the rootes of an equation beare to one another.
20 One line being to find other lines at {pleasure} of {illeg} {same length} {illeg}
21 How much doth any medium resist the motion of any given body.
22 To Determin maxima & minima in equation which hath more than {illeg} unknowne quantitys.
To Determin max & min by numbers.
< text from higher up f 4r resumes >[27] . . . . . . . . . . . . . . . . . . . . . . . .
[28] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . { 8 } . . . . . . . . . . . . . . . .
<5r>— − . . . 15. . . . {14} . . . . {illeg} {illeg} . {illeg} . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . 4 . + 120 [29] . 102 { 2 }620 1 {illeg}
[30] . . . {illeg} . . . . . {illeg} . {3 } . . . . {illeg}+{illeg}={illeg}. . {illeg} {illeg} {illeg} = {illeg}{illeg}{illeg}. {illeg} {illeg}{illeg} {illeg}{illeg}{illeg} {illeg}
<5v> < insertion from the bottom of the page > < text from f 5v resumes >
. .
.
. . . . . r ♉x
♉x

 for x
write for
y
write
{illeg}
r
x
♉
for
y
♉ {illeg}
z
for x
write for
y
write
{illeg}
r
x
♉
for
y
♉ {illeg}
z

 2
2
 2
{illeg}
2
{illeg} {illeg}
{illeg} 
 ♉ ♉2
{illeg}
z
♉ ♉2
{illeg}
z


 {illeg} {illeg}−{illeg}
{illeg} {illeg}−{illeg}
[34] . . . . . . . . . . . . .
. . . . . . . . . . . . .
[35] . . . .
.
. . . . . .
. . . . . . . . . . . . . . . . therefore take , & the greatest crookedness of the line cb will be found at b . . . . . . . . . . {illeg} . . . as before. or . . . . . . . . . . . . [36] . .
<6v>[37]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
any finite line. as .
.
.
.
.
.
.
.
,
.
.
. .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
a
. Or
.
.
.
.
.
. 5
.
.
.
.
.
.
.
.
{illeg}

. . . . .
.
.
.
.
 . .
. .
.
.
.
☞ To know whether the changing of the signes of an Equation change the nature of the crooked line signified by that Equation observe that
If the signes of every other terme (of that Equation ordered according to {either} of the undetermined quantitys) be changed the nature of the line is not changed. but if some signes bee changed but not in eve{ry} other terme (of it ordered according to one of the unknowne quantitys) the nature of the line is changed.
If the knowne quantitys are every where divers, & one of them be blotted out that produceth a line, when one terme is already wanting
Those lines may bee defined the same whose natures may be expressed by the same equation although angles made by x & y are not the same.
In the Hyperbola the area of it beares the same respect to its Asymptote which a logarithme {di}{illeg} number.
To make the equation . be divisible by . suppose , then tis . therefore write c in steade of a & it is . which is divisible by To make the same Equation divisible by Suppose it to bee divided by it & the ration will bee . The quote is which have vanished therefore to make soe suppose each terme & the{illeg} will be & both include . Which since it cannot happen the equation cannot be divided the one by the othe{r}
The rootes of two divers equations may easily be added to substracted from multiplyed {&c} by one another while they are unknowne.
[38] That the penultimate terme of the Equation . bee wanting I multiply & then suppose x a knowne quantity & y an unknowne {illeg} {illeg} {illeg}{ .} by this {having}{illeg} x {illeg} {illeg} {illeg}
[39] . {} [40] [41] [42] . . . . [43] . [44] . . . . . . . . [45]
<8r>[47] . . . . . . . z. . . . . . . . . . . . . . . . . . . . . .
[48] . . . . . . . . . . . . . . . Lastly . . . & Therefore . & .
[51]
. . . . . x y . . in the 1st case.[52] . . in the 2d case.[53] . .
[54] Haveing the nature of a crooked line expressed in Algebraic termes to find its axes, to determin it & describe it Geometrically &c
[55] If . . & y being perpendicular to x describes the crooked line the line with one of its extremes. Then reduce the Equation (expressing the nature of the line ) to one side soe that it be . ☞ Then find the perpendicular bc which is done by finding . for (In finding observs this rule. Multiply each terme of the Equation by so many units as x hath dimensions in that terme, divide it by x & multiply it by y for a Numerator. Againe multiply each terme of the Equation by soe many units as y hath dimensions in each terme and divide by for a denominator in the valor of v. [56] Example, . . . therefore . Also if . [57] And if . then . &c) Then make . . . & substitute this valor of into the place of x & this valor of into the place of y in the Equation & there take {in} a 2d equation. then by multiplication or by some other meanes take away the irrational quantity & lastly take awa{y} y or x by the helpe of these 2 Equations, soe that you have a 3rd equation in which there is either x onely, or y onely & supposeing it to have 2 equall roots multiply it according to Huddenius his Method for a 4th Equation & by the helpe of the 3rd & 4th equation take away the unknowne quantity viz: either x or y. & there will result a 5t Equation in which is neither x nor y. & by which the valor of z may be found. The greatest of whose valors signifies the longest, the least of them the shortest of all the perpendicular lines ab. & if it have other rootes they signifie other lines which are perpendicular to the crooked line at both ends, a & b; & some of these must signifie the axes of the line if it bee of an elliptical nature.
[58] . . z . ϩ . . . . . . ed
.
Haveing therefore an equation expressing the nature of a crooked line To find its axis. Supposeing some quantity most frequent in the equation Subrogate into the roome of x ; & into the roome of y: Order the Equation according to ϩ, make every terme , in which ϩ is of one dimension Order every terme in this secondary Equation according to the dimensions of z. & supposeing every terme of each of them , by the helpe of these Equations (in which is neither x , y , z or ϩ ) may be found the valors of a & b . Then perpendicular to ac from the point a draw . & from the point b draw , & parallel to ac. from the point k draw , & perpendicular to bk . & through the points b , m draw bl the axis of the line hgn . & that the relation twixt z. & may bee had, write the valors of a , b , c now found in their stead in the secondary equation.
Example . Then makeing I write , or for x & its square for &c. & for y , & its square for . & soe I have this equation, or by ordering it according to ϩ , Then by makeing those quantitys in the last terme save one . I have this Equation . Which I divide into 2 parts makeing those termes in which z is not, & those in which z is of one dimension. & then I have these 2 equation{s} . & . by the first . Or . That is . by the 2d Equation I find . or . & by writing the valor of which was found before I have . Or . Or . & or . & .
[60] . . . . . . . . . . . . . . . . . . . . . &c . .
[61] If any crooked line be revolved about its owne axis it generates a Sollid intersected by any plaine not perpendicular to the axis produceth another line the former. But if it bee revolved by any other line it generates a Sollid which intersected by any plaine not perpendicular to the axis produceth another whose composition is {n}ot to the formere
 In the triangle
adb
if , & are definite, but , & indefined. Then the Equation is . But in this case the maximum or minimum of either v or x cannot bee found according to Cartes or Hudde{nius} method, by reason that hath not 2 divers valors when is determined, which become equall when is the least or greatest that may be. But
cd
might have bee used inste{ad} of
cb
&c. There be other instances of this Nature against Huddenius his assertion.
In the triangle
adb
if , & are definite, but , & indefined. Then the Equation is . But in this case the maximum or minimum of either v or x cannot bee found according to Cartes or Hudde{nius} method, by reason that hath not 2 divers valors when is determined, which become equall when is the least or greatest that may be. But
cd
might have bee used inste{ad} of
cb
&c. There be other instances of this Nature against Huddenius his assertion.
 These points a,b,c, being given a circle may be described (which shall pass through them all) by an instrument whose angle . And soe the sides ed & df being moved close by the points a & c, the point shall describe the arch abc
These points a,b,c, being given a circle may be described (which shall pass through them all) by an instrument whose angle . And soe the sides ed & df being moved close by the points a & c, the point shall describe the arch abc
To worke mechanically & exactly by a {scale} it may bee better divided according to the fassion represented by the figure A, then by that at B.
To make a {plated} superficies exactly: Take three plates A, B, D.  & {grind} them together A & B, A & D, B & D; pressing the uppermost plate onely in the middle at c that it may not weare {move} away in the edges than in the midst & move it to & fro with but small vibrations. Soe shall the 3 fiduciall sides of the 3 plates bee {ground} exactly plane.
& {grind} them together A & B, A & D, B & D; pressing the uppermost plate onely in the middle at c that it may not weare {move} away in the edges than in the midst & move it to & fro with but small vibrations. Soe shall the 3 fiduciall sides of the 3 plates bee {ground} exactly plane.
[62] Probleme. Of Usury. the principle. bc= the time of the money lent the use due for the principle for the time bc. the use upon use. the use for the principle & use during the time bc. . df a tangent to the line bd. dg a perpendicular. . Then as the summe or principle drawne into the time bc, is to the use for it in that time [63] So is the summe drawne into the time fc, to the use for it in the time fc. therefore . . . . . .
Of Reflections.
[64] Of Reflection.
 Suppose the Bodys a, b doe not reflect one another but conjoyne at theire meeting & soe move or rest together. the body a; the body fec; body ced; body fedc. motion of , motion of , motion of , motion of , before reflection. motion of , motion of , motion of , motion of after reflection. swiftnesse of , motion of , , or , before reflection swiftnesse of , swiftnes , , or occursion. ⊙ the point of theire occursion.
Suppose the Bodys a, b doe not reflect one another but conjoyne at theire meeting & soe move or rest together. the body a; the body fec; body ced; body fedc. motion of , motion of , motion of , motion of , before reflection. motion of , motion of , motion of , motion of after reflection. swiftnesse of , motion of , , or , before reflection swiftnesse of , swiftnes , , or occursion. ⊙ the point of theire occursion.
Axiome 1st
Two bodys being alike swift the motion of motion . for equall parts have equall motion. Therefore all the parts of all such parts of motion the motion of c.
Prop: 1st. If before the occursion of a & d a rest then shall . & since , tis {alsoe} . Or also .
Prop: 2d. If a meete d, & have lesse motion than it, then, . for suppose, . then should a & b rest after occursion did not force them towards k.
Prop 3 suppose i the center of gravity in d, y in a. z & f the in which the bodys a & d touch in theire meeting. ⊙ the point of theire meeting. the magnitude of the body , the magnitude of d. motion of a before meeting, motion d before meeting. the time in which a or d  moves to time in which they both move to y. motion of a, motion of d after occursion . . or . . .
.
moves to time in which they both move to y. motion of a, motion of d after occursion . . or . . .
.
 magnitude of the body a, magnitude of the body d. {illeg} {illeg} the point of concourse: the points of contact, at o. b. . . time in which the bodys move from z & f to o. time in which they move from o to p. motion of a before occursion motion of d after occursion {illeg} or . & {illeg}. . {illeg}
.
magnitude of the body a, magnitude of the body d. {illeg} {illeg} the point of concourse: the points of contact, at o. b. . . time in which the bodys move from z & f to o. time in which they move from o to p. motion of a before occursion motion of d after occursion {illeg} or . & {illeg}. . {illeg}
.  . {illeg}{&} d meete {illeg} {illeg} that c must be negative that is {illeg}e be negative the point {illeg} must be t{illeg}on the same side {illeg}
. {illeg}{&} d meete {illeg} {illeg} that c must be negative that is {illeg}e be negative the point {illeg} must be t{illeg}on the same side {illeg}
Definitions.
[66] 1st When a body Quantity from one parte of Extension to another it is saide to mo{ve.}
2 One body Quantity is soe much swifter than another, as the distance through which it passeth is greater than the distance through which the other passeth in the same time.
3 One Quantity hath so much more motion than another, as the distance through which it moveth drawne into its quantity, is to the distance trough which the other moveth in the same time drawne into its quantity. As if the line ab move the length of bc  & ef the length of eh in the same time, the motion of ab is to the motion of cd, as , to .
& ef the length of eh in the same time, the motion of ab is to the motion of cd, as , to .  Alsoe if the cube move the length of ; & the piramis move the length of in the same time; then, as,
the motion of lmqyz to the motion tvwx. Or the motion of one quantity to another is as their powers to persever in that state
Alsoe if the cube move the length of ; & the piramis move the length of in the same time; then, as,
the motion of lmqyz to the motion tvwx. Or the motion of one quantity to another is as their powers to persever in that state
Those Quantitys are said to have the same determination of their motion which move the same way, & those have divers which move divers ways.
[67] 5 A quantity is reflected when meeting with another quantity it looseth the determination of its motion by rebounding from it. As if the bodys a, b meete one another in the point c they are parted  either by some springing motion in them selves or in the matter {crouded} betwixt them. & as the spring is more dull or vigorous quick soe the bodys will bee reflected with th more or lesse force; as if it endeavour to get liberty to inlarge it selfe with as greate strength & vigor as the bodys
, pressed it together, the motion of the body a from b will bee as greate after as before the reflection. but if the spring have but halfe that vigor, then the distance twixt a & b,at the minute after the reflection shall bee halfe as much as it was at the minute beef{ore} the reflection.
either by some springing motion in them selves or in the matter {crouded} betwixt them. & as the spring is more dull or vigorous quick soe the bodys will bee reflected with th more or lesse force; as if it endeavour to get liberty to inlarge it selfe with as greate strength & vigor as the bodys
, pressed it together, the motion of the body a from b will bee as greate after as before the reflection. but if the spring have but halfe that vigor, then the distance twixt a & b,at the minute after the reflection shall bee halfe as much as it was at the minute beef{ore} the reflection.
 7 Refraction is when the body c passing obliquely through the surface ed at the point b meets with more opposition on one side of the surface than on the other & soe looseth its determination; as if it turne towards a.
7 Refraction is when the body c passing obliquely through the surface ed at the point b meets with more opposition on one side of the surface than on the other & soe looseth its determination; as if it turne towards a.
[68] 9 Force is the pressure or erouding of one body upon another,
10 The center of { Motion } in the same body is such a point within a quantity which rests when a body is moved with any circular but noe progressive motion; also the line in n drawne through it is called an axis of motion.
The center of motion in 2 divers bodys is a point soe placed twixt those bodys that (if it bee conceived to rest ) if the bodys bee moved about it with circular motion they shall both have an equall quantity {o}f motion, the line about which they move is the axis of motion.
12 A Body is said to move toward another body either when all its points move towar{d}s it or else when some of its points have more motion towards it than others have from it. Otherwise not
< insertion from the left margin >13 Bodys are more or lesse distant as the distances of their centres of motion are more or lesse. or as their distances might bee acquired with more or less motion
< text from f 10v resumes >Axiomes. Propositions.
1 If a quantity once move it will never rest unlesse hindered by some externall caus{e.}
2 A quantity will always move on in the same streight line (not changing the determination {nor} celerity of its motion) unlesse some externall cause divert it.
3 There is exactly required so much & noe more force to reduce a body to rest as there was {to} put it {illeg}n motion: et e contra.
4 S{illeg} much {illeg}{illeg}s is required to destroy any quantity of motion in a body soe {illeg} to generate it; & soe much as is required to generate it soe mu{illeg}ived to destroy it.
[69]6 {illeg}ove 2 unequall bodys (a & b) the swiftnesse of one body is to the s{illeg} is to a . {(1)} & therefore the motion of both bodys shall bee equall.
5 If {illeg}{b}ee moved by unequall forces, as the force moveing is to the force {illeg} motion of b. to the m{illeg} of c, so is the swiftnes of b, to that of c.
[70]7 If two body {illeg}{illeg} {illeg}way to{illeg}s {illeg}{illeg}r{illeg}cking {illeg} {illeg}e of theire motion shall be lost. f{illeg} pres{illeg}{illeg}{illeg}{illeg} the motion of shall {illeg}{illeg}
[71] 8 If two quantitys (a & b) move towards one another & meete in o, Then the difference of theire motion shall not bee lost nor loose its determination. For at their occursion they presse equally uppon one another, & (p)[72] therefore one must loose noe more motion than the other doth; soe that the difference of their motions cannot be destroyed.
[73] 9 If two equall & equally swift bodys (d & c) meete one another they shall bee reflected, soe as to move as swiftly frome one another after their reflection as they did to one another before it. For first suppose the sphæricall bodys to have a springing or elastick force soe that meeting one another they will relent & be pressed into a sphæroidicall figure, {&} in that moment in which there is a period put to theire motion towards one another theire figure will be most sphæroidicall & theire pression one upon the other is at the greatest, & if th{e} endeavour to restore theire sphæroidicall figure bee as much vigorous & forcible as theire pressure upon one another was to destroy it they will gaine as much motion from one another their parting as they had towards one another theire reflection. Secondly suppose they be sphæricall & absolutely sollid then at the period of theire motion towards one another (that is at the moment of theire meeting) theire pression is at the greatest or rather tis done with the whole force by which theire motion is stopt, for theire whole motion was stoped by the force of theire pressure upon one another in ysone moment & there cannot divers degrees of pressure twixt two bodys in one moment) Now so long as neither of these 2 bodys yeild to one another they will retaine the same forcible pressure towards one another: that is soe much force as deprived the bodys of their motion ( towards one another soe much doth now urge them from one another, & therefore (r)[74] they shall move from one another as much as they did towards one another before theire reflection.
10. There is the same reason when unequall & unequally moved bodys reflect, that they should seperate from one another with as much m{ot}ion as they came together.
[75] [76]
 11 If a line be bisected in about which the line doth circulate & that point bee fixed. then the whole line hath noe progressive motion. For makeing , bf, ag, & dh bee parallel, & perpendic to fh, then is . & . Wherefore the point c moveing towards n the point d shall move soe much towards the line fh as the point b doth from it, & all the points in or the line ac move as much to the line fh as all the points in or the line moves from it soe that the whole line ce stays in equilibrio neither moveing to nor from fh, by the 12th Defin.
11 If a line be bisected in about which the line doth circulate & that point bee fixed. then the whole line hath noe progressive motion. For makeing , bf, ag, & dh bee parallel, & perpendic to fh, then is . & . Wherefore the point c moveing towards n the point d shall move soe much towards the line fh as the point b doth from it, & all the points in or the line ac move as much to the line fh as all the points in or the line moves from it soe that the whole line ce stays in equilibrio neither moveing to nor from fh, by the 12th Defin.
12 Hence when the center of a line is not in the midst of a line the whole line moves the same way which the longest parte doth. for supposeing then the line ce in equilibrio (per axiom:11) but if moves towards & be added to then moves towards ce (by def {12}
13. When moves circularly but maketh noe progression its middle point shall rest & is therefore the center of its motion, for if the middle point move let it bee to r from a soe that the line ec bee moved into the place {} then let the {} move about the fixed center r into the place xs, then {xs} & {wt} are equally distant from fh (by definition 13 & axiom 11) & alsoe & are equally distant from the {illeg}{am} f{illeg} but xs & ln are not equally distant from f{illeg}{illeg}ore neither are wt & ce equally distant from fh. & therefore the line {illeg} pro{gre}ssive motion when it {pressed} into {wt}
14 By the same reason the middle point {illeg}ogram, parallelipipedon, prisme cilinder, circle, sphære, elipsis, sphæroides {illeg} of theire motion
<11v>[77]
14 A Body being moved parallell to its selfe all its points describe parallel lines, & each them have the same determination & velocity with the body. for (by axiome 2d) they must all bee streight ones which if they intersect the body will not be moved parallel to its selfe. &c.
[78] 17 If a body move streight forward & circularly its center of motion shall have the same determinacon & velocity that the body hath. For {suppose} ac to be moved into the place gh & its center of motion b into the place d, then let it turne about the center d into the place ef parallel to to ac soe that the point which was in bee now in . Now since {} by moveing into the place makes noe progressiv motion (definition 10) it follows that the same quantity (Or since ) the same velocity & (axiom 10) determination of motion in the same time would translate ac parallell to it selfe into the place ef that would translate it into the place gh , had it both progressive & circular motion. But the point d hath the same velocity & determination which the line ef hath when moved parallel to its selfe (x)[79] therefore the point d hath the same determinacon & velocity which the line gh hath when moved with both circular & progressive motion vide axiom 37.
18 If a body move progressively in some crooked line & alsoe circularly its center of motion shall have the same determination & velocity which the body {hath} for (axiom 17) this is trew when its motion is in a streight line but a crooked line may bee conceived to consist of an infinite number of streight lines. Or else in any point of the crooked line the motion may bee conceived to be on in the tangent.
[80] 19 If 2 bodys make the same number of circulations with the same dista{nce} from the center c : then as the Radij of the circles which their centers of motion describe are to one another soe are the perimeters one to another soe are theire velocitys one to another (axiom 10, definition 2), & their motions are to one another as theire bulkes drawne into the Radij of those circles (which theire centers of motion describe) are to one another (definition 3). As: velocity of velocity of ac. & motion motion of ao.
[81] 20 If a sphære ⊙c move with in the concave sphæricall or cilindricall surface of the body edf circularly about the center m it shall press upon the body def for when it is in c (supposeing the circle bhc to be described by its center of motion & the line cg a tangent to that circle at ⊙) it moves towards g or the determination of its motion is towards c therefore if at that moment the body edf should cease to check it it would continually move in the line cg (axiom 1. 2.) obliqly from the center m , but if the body def oppose it selfe to this indeavour keeping it equidistant from m , that is done by a continued checking or reflection of it from the tangent line in every point of the circle chb , but the body edf cannot check & curbe the determination of the body c⊙ unless they continually presse upon one another. The same may be understood if the body adb bee restrained into circular motion by the thred
21. Hence it appeares that all bodys moved circularly have an endeavour from the center about which they move, otherwise the body ⊙c would not continually presse upon edf .
22 The whole force by which a body c⊙ indevours from the center m in halfe a revolution {i}s more than double to the force which is able to generate or destroy its motion for supposeing it have moved from by to then the resistance of the body ef (which is equall to its pressure upon def ) is able to destroy its force of moveing {illeg}{illeg} & to generate in it as much force of moveing from to the qu{illeg}g way.
[82] 2{5}{3} Having {illeg}of motion of the 2 bodys ob & dc to find the common center of both {in}{illeg}draw a line ⊙e from the centers of theire motions ⊙ & e & divi{illeg}oe that the body ob is to the body de as the line ae to the line oa : that is soe{illeg} . For then if they move about the center {illeg}{illeg}{illeg} they have equall motion (axiom 19th) & consequen{tly} {illeg} have an equall endeavour from the center a (axiom 23) soe that if they bee joyned to center by the lines ae & ao the one hindereth the other from forcing the center a any way soe that it shall stand in equilibrio betwixt them & (by definition 10) is therefore their center of motion
[83]
24 If two bodys ( cb & de move about a center then ∼ ∼ ∼ ∼ ∼ ∼ The whole force by which the body cb tends from the center a in one revolution being equall to {6}{61} times the force by which that body is moved (axiom 22) is to the motion of that body as the whole force by which the body de tends from the center a in one revolution (which is equall to 6{+} times the force by which the de is moved, or which is able to stop its motion (axiom 22) ) is to the motion of the body de . Vide Axioma 23ũ.
[84] 26 If the body a move through the space ab in the time d , & the body c through the space cd in the time f . then the velocity of a is to the velocity of c as to be . For supposeing that . then is And (by definition 2) the velocity of is to the velocity of
[85] Alsoe the motion of a is to the motion of c (by definition 3d) .
Note that when the motion is uniforme that is when a body moves over the same space in the same time (which will ever bee when the motion of that body is neither helped nor hindred) then in a right angled triangle a b may designe the space through a body moveth in the time eb. Otherwise when tis not uniforme the proportion of the time in which a body moves to the distance through which it moves may be designed by lines drawne to a crooked line, as the time by gf & ih , the distance by gh or fi , the velocity by the proportion of nh to hi , ni being tangent to the crooked line at i . &c.
[86] 23
If the body
bace
acquire the motion
q
by the force
d
& the body
f
the motion p by the force
g
. then
. for suppose the body
, to acquire the motion
w
by the force
d
, then (axiom 5)[87]
. but
(by axiom 4) therefore .
Axiom {1}00 Every thing doth naturally persevere in that state in which it is unlesse it bee interrupted by some externall cause, hence axiome 1st, & 2d, & {γ}, A body once moved will always keepe the same celerity, quantity & determination of its motion.
[88]
101 . Supposeing the bodys aobc & cbqp to be equall & equivelox: Then that cause hindrence, impediment resist{ance} or opposition which can onely deprive cbqp of its whole velocity & motion by hindering its p{er}severance can also onely deprive aocb of its whole {whole velocity &} motion {illeg} that caus hath the same {illeg}{illeg} over both the bodys. Now if {illeg} add the opposition which can {being} {illeg}ive of its {illeg} reduce cbpq to {illeg}{illeg}ion which can reduce aob {illeg} {illeg} the whole opposition ( ) {illeg} {illeg} both {illeg} bodys ) {illeg} {illeg} motion when they are joyned into one for Also neither {illeg} a or b {illeg} aopq of {illeg} motion for {illeg} parte ( a or b ) would be equall to the whole ( ). By the same reason aopq & cbqp loosing equall velocity the impediment of aopq must be double to the opposition of cbpq .
[89] 102 Since beacuse aopq is double to cbpq & both of them equivelo{x} therfore the opposition which can deprive aopq of its motion must be double to that which can deprive cbpq of its motion; by the same reason it will follow that in equivelox bodys as one body is to another soe must the resistance which can deprive that body of its bee to the resistance which can deprive of its whole so is the resistance which can deprive of some parte of its velocity, to the resistance which can deprive of the same quantity of velocity, soe that a & b bee still equivelox.
103 By the same reason alsoe If two bodys rest or bee equivelox: then as the body is to the body soe must the power or efficacy vigor strength or virtue of the cause which begets new velocity in bee to the power virtue or efficacy of the cause which begets the = same quantity of velocity in b , soe that a & b bee still equivelox.
104 Hence it appeares how & why amongst bodys moved some require a more potent or efficacious cause others {a lesse} to hinder or helpe their velocity. And the power of this cause is usually called force. And as this cause useth or applyeth its power or force to hinder or change the perseverance of bodys in theire state, it is said to Indeavour to change their perseverance.
[90] 105 If the equall & equivelox bodys a & b meete (unlesse they could passe that one through the other by penetrating its dimentions) they must necessarily hinder the one the others progression, & since these bodys have noe advantage the one over the other the hindrance on both parts will be equall, likewise if the bodys & bee equall & equivelox they must equally hinder one anothers progression But the body (being lesse than the body & equivelox with ) cannot hinder the progression of the body soe much as the body can; for {then} the power of being part of the power of the body would bee equall to the whole power of therefore that & being equivelox doe equally hinder the one the others progression tis required that they be equall.
[91] 106 Now if the bodys a & b meete one another the cause which hindereth the progression of a is the power which b hath to persever in its velocity or state & is usually called the force of the body b & is soe that a body is {so} to be moved with more or lesse force which meeting with another body can cause a greater or lesse mutation in its state, or which requireth more or less force to destroy its motion. & as {one} body b useth or applyeth this force to stop the progression of a it is said to Indeavour to hinder the progression of a which indeavour in body is performed by pressure & by the same reason the body b may bee said to endeavor to helpe the motion of a if it should apply its force to move it forward: soe that it is evident what the Force & indeavor in bodys are.
[92] 107 If the bodys b & c be equivelox then as the force with which b is moved (or the power of b to persever in its velocity or to {keepe}{helpe} {illeg} hinder another body from persevering in its velocity to the force of c . For let there be 2 other bodys a & d equivelox to them soe that a meeting b , & d meeting c they would eqaully hinder one others progression then is , & (axiom 105) & then force which can stop (= to the force of b ) to the force which can stop d (= to the force of c ). (vide axiom 102.
[93] 108 Tis knowne by the light of nature that equall forces shall effect an equall change in equall bodys. Therefore if the forces g, h, k, m, be equall, & the bodys a, b, equall & rest, then let bee moved by the force g ; & b by h , a & b shall be equivelox: Also (since tis noe greater change for to acquire another part of motion now it hath one than for it to acquire that one when it had none) if bee againe moved forward by the force k , its velocity shall be double to the velocity of b , & if it bee againe moved forward by the force m its velocity shall be triple to that of b . &c. Whence as the force moving is to the force moving soe is the velocity acquired in to the velocity acquired in {by that force}
109 By the same reason if & the velocity of a be triple to the velocity of b , that force can deprive a of its velocity. which is triple to the force which can deprive b of its velocity. Or in generall {2} so is the lost velocity of a to the lost velocity of b As the force which deprives a of some or all of its velocity, to the force which deprives b of some or all of its velocity
[94] 112 A body is saide to have more or lesse motion as it is moved with more or lesse force, that is as there is more or lesse force required to generate or destroy its whole motion.
[95] 113 If a body move through the space ab in the time c . & the body f through gf in the time h then, time time line ab ak . & the body a would move through the space ak in the same time in which the body f moves through the space fg . Therefore the velocity of a is to the velocity of f as the line line fg (definition 2) Then I add the body r to f soe that . since f & r are equivelox, (axiom 107) as force or motion of f , to force of . againe since , (axiom 111) as the velocity of a ; to the velocity of the force or motion of a , to to the force of . Soe that, . Soe that haveing any 7 of these the 8th may bee found. but suppose the bodys moved in equall times that is if , then the rest of the termes may bee found by, . &c. that is as is to soe is the motion of the body f to the motion of the body a . &c.
[96] 110. If the bodys (
a
&
b
) bee equall & the celerity of
a
triple to that of
b
, then if the force
d
can deprive
b
of its motion, the force
can deprive
a
of its motion. But if there bee lesse force
it cannot deprive
a
of its motion for soe the parte
would be = to the whole
; if there be more force
it will doe more than deprive the body
a
of its motion (i.e. move it the contrary way) otherwise the parte
would be equall to the whole
. Therefore the
force which can deprive
a
of its motion must bee triple to the force which can deprive
b
of its motion & consequently (definition 106) the force wherwith
a
is moved is triple to the force wherewith
b
is moved
111 By the same reason as the celerity of the body is to the celerity of b so is the force wherewith a moveth to the force wherewith b moveth.
[97] 114 There is required soe much & noe more force to reduce a body to rest than there is to move it: et e contra. And
115 Soe much force a is required to generate any quantity of motion in a body so much is required to destroy it, & e contra. For in loosing or to getting the same quantity of motion a body suffers the same quantity of mutacon in its state, & in the same body equall forces will effect a equall change
[98] 116 If the bodys , a & b are moved with the same force then the celerity of b is triple to the celerity of a . for moved by is equivelox to b moved by d , but since , therfore a moved by is equivelox to b moved by d . And (axiom 108) as the celerity of a moved by d is to the celerity of a moved by , soe is 1 to 3 , soe is the celerity of a moved by d to the celerity of b moved by d .
By the same reason, Any bodys f & g being moved by the same force as is to , soe is the celerity of to the celerity of acquired by that force. tis axiome the 4th And (by axiom 113) the bodys will have equall motion.
[99] 118 If the body p , be moved by the force q , & r by the force s , to find the celerity of p & that of r , I add to p , soe that , & that , & are moved with equall force, then the celerity of , (axiom 117) alsoe, (axiom 108) . Or . that is the celerity of p is to the celerity of r as is to . And by axiom 113 the motion of p is to the motion of r as the force of p to the force of r . And by the same reason if the motion of p & r bee hindered by the force q & s , the motion lost in p is to the motion lost in r , as q is to s . or if the motion of p be increased by the force q , but the motion of r hindered by the force s ; as q , to s proportional so is the increase of motion in p , to the decrease of it in r (axiom 111
[100] 121 If 2 bodys p & r {nest} the one the other, the resistance in both is the same for soe much as p presseth upon r so much r presseth on p . And therefore they must both suffer an equall mutacion in the motion.
119 If r presseth p towards w then p presseth r towards w . {illeg} without {illeg}
120 A body must move that way which it is pressed.
122 Therefore if the body p comes from c & the body r from d soe much as { p {illeg} } motion is changed towards w soe much the motion of {illeg} changed {illeg}{illeg}
<13v>[101] 27 If two bodys b & c move from their center of gravity they shall have equal motion For suppose b moved into the place d ; then putting, (axiom 25) the body c must be then moved into the place e . Alsoe . (axiom 25) therefore . that is . But (axiom or) the motion of c , to the motion of d , & therefore c , & d have equall motion towards o
[102] 28. If two bodys b & c mov in the lines br & cr . The body c moveing through the space cg in the time vs , & though g h in the time nv , & through kr in the time nr . & the velocity of the body b is to the velocity of c as d , to e , & as the line cg to the line be , or as ck to br , then when the body c is in the place g , b will bee in e , & when c is in k , b will be in r . to find the line which the center of their motion describes, viz dfo . Then nameing the quantitys , . . . . If o be the center of motion of the bodys at k & r ; then, . And the line df must passe through o . againe making . then . & if , then . &, . . since f is the center of motion in the bodys at g & e tis, . . . . . . . [103] Now if the lines . Then the line od must be a streight line. but . therefore the line do is a streight line, with which may bee found by the two points d & o . The demonstracon is the same if the body b moved from a to b
 29 If two bodys
q
&
c
be moved in divers plaines, then find the shortest line
which can bee drawne frome one line
to the other line
in which those bodys are moved, & that line
pr
shall bee perpendicular to both the lines
cr
&
qp
, viz
. then draw
qb
equall &
& draw
. Then shall the plaine
qbrp
be perpendicular to the plaine
bcr
. Suppose also the body
c
moves over the space
& that the body
q
moves over the space
qa
in the time
vw
, &
ap
in the time
wt
. Also suppose another body
& equivelox to {
} that is to move over the space
in the time
vw
{illeg}
29 If two bodys
q
&
c
be moved in divers plaines, then find the shortest line
which can bee drawne frome one line
to the other line
in which those bodys are moved, & that line
pr
shall bee perpendicular to both the lines
cr
&
qp
, viz
. then draw
qb
equall &
& draw
. Then shall the plaine
qbrp
be perpendicular to the plaine
bcr
. Suppose also the body
c
moves over the space
& that the body
q
moves over the space
qa
in the time
vw
, &
ap
in the time
wt
. Also suppose another body
& equivelox to {
} that is to move over the space
in the time
vw
{illeg}
Soe that when is in or , will bee in or & in or . Then Then drawing {the} streight lines qc , ag , bk if , the points d , f , & o , shall be the centers of motion of the bodys b & c , when they are in the places b & c , e & g , r & k . & (proposition 28) therefore the line ( dfo ) in a streight line. Likewise if it bee , then the points l , m , n are centers of motion to the bodys ( q & c ) being in the places & , a & g , p & k . Then drawing the lines ld , mf , no , (twixt the neighbouring centers of motion) since {bc }. therefore & by the same reason & . Wherefore all the lines qb , ae , pr , ld , ml , no are parallell to one another. And , soe that . & since these lines ld , mf , no , are parallell, equall, in the same plaine ldon , & stand upon the same streight line do , the line in which their other ends l , m , n , are are terminated (i.e. in which are all the centers of motion of the bodys ( c & q )) must bee a streight line.
The demonstracon is the same if moved from to .
[104]
[105]
[106]28 & 30th. The bodys ( b & c ) being in b & c , e & g , r & k , in the same times, & d n being described by their centers of motion. Also making . & . Then (for the motions of b & c are uniform) (for ) . Againe (for (proposition 25)). Therefore & consequently the points d f n are in one streight line. also since the center of motion must bee uniforme.
[107] 31 If two bodys ( b & c ) meete & reflect one another at their center of motion shall bee in the same line after reflection in which it was before it. For the motion of b towards d the {center} of their motion is equall to the motion of c towards d , by proposition 25. then drawing { } & { }. then . therefore the bodys b & c have equall towards the points k & { c }. that is towards the line kp . And {illeg} {illeg} reflection so much as presseth from the {illeg} after reflection that is {illeg} {illeg} . { } & {illeg} {illeg} tis {illeg} equall {illeg} the {illeg} must therefore be the center of motion of the bodys b & c when they are in the places g & e . & it is in the line kp . The Demonstracon is same in all cases.
[108] 32  If the bodys (
b
&
c
) reflect at
q
to
e
&
g
, & the center of their motion describe the line
kdop
. the velocity of that center
after reflection shall bee equall to the velocity of that center
before reflection. For from the center
draw the lines
af
perpendicularly to
kp
. & suppose the line
af
to have the same celerity which (the point
d
) the center of motion hath before reflection, soe that when the bodys (after reflection are in
e
&
q
, the line
af
may bee in
kr
. Also draw
ab
. Then since
d
is the center of motion in
&
, the bodys
&
have equall motion towards
d
, but,
. Therefore, the bodys
&
have equall motion towards
a
&
f
that is towards the line
adf
. Now when the bodys reflect, so much as the body
b
presseth the body
c
from the line
af
(or
sf
) or towards
p
soe much the body
c
presseth the body
b
from the same line, or towards
k
, (by x axiom 119) therefore the bodys
b
, &
c
, have equall motion from the line
af
, after reflection (by axiom 121) that is when are at
e
&
g
they doe equally move from the points
h
&
r
; then drawing
eg
, tis
. Therefore the bodys doe equally move from the point
which (by axiom 25) must bee their center of motion, & since the motion of the line (
af
or
hr
) is uniforme (by supposition) & the point
o
is in the line
hr
, & also in
kp
(by proposition 31.) its motion must be uniforme.
If the bodys (
b
&
c
) reflect at
q
to
e
&
g
, & the center of their motion describe the line
kdop
. the velocity of that center
after reflection shall bee equall to the velocity of that center
before reflection. For from the center
draw the lines
af
perpendicularly to
kp
. & suppose the line
af
to have the same celerity which (the point
d
) the center of motion hath before reflection, soe that when the bodys (after reflection are in
e
&
q
, the line
af
may bee in
kr
. Also draw
ab
. Then since
d
is the center of motion in
&
, the bodys
&
have equall motion towards
d
, but,
. Therefore, the bodys
&
have equall motion towards
a
&
f
that is towards the line
adf
. Now when the bodys reflect, so much as the body
b
presseth the body
c
from the line
af
(or
sf
) or towards
p
soe much the body
c
presseth the body
b
from the same line, or towards
k
, (by x axiom 119) therefore the bodys
b
, &
c
, have equall motion from the line
af
, after reflection (by axiom 121) that is when are at
e
&
g
they doe equally move from the points
h
&
r
; then drawing
eg
, tis
. Therefore the bodys doe equally move from the point
which (by axiom 25) must bee their center of motion, & since the motion of the line (
af
or
hr
) is uniforme (by supposition) & the point
o
is in the line
hr
, & also in
kp
(by proposition 31.) its motion must be uniforme.
Note that by this, & the 31th proposition I can find the center of motion of two bodys at any given time; & by proposition 9, or definition 5th, I can find their distance, & by proposition 25, their distance from their center of motion. that is the 2 spheres in whose perimeters they be found; There wants therefore onely their determination to bee knowne that their places in the spære may bee found.
[109] 33 Suppose the body dcgk immoveable, the surface dcg being plaine. Also let the sphæricall body amn bee moved in the perpendicular ch . so as to be reflected in c Then since the side am hath as much force to weigh or presse towards as the side an to presse towards e by reason that a the center of its motion is in the line ch ( ) the body must be in equilibrio neither pressed towards d nor e but reflected back in the line ch . The same may be said of any bodys whose motion center is in the perpendicular to the reflecting point.
[110] 34 Take . soe that . Then draw the perpendiculars eb , fc , gd , hm . And Set a body upon the points a & m & let stand on the points e & k which are in the perpendiculars eb , & hkm , & fh , on the points f , & h & lay a Globe let the same be supposed of hkm . Then suppose (for distinctions sake have 8 parts of force, with which it presseth fh . Then must fh presse with 8 parts of force, that is (since , or ) with 4 parts on the point h , & with 4 on the point f upon the body efk , so that efk must presse with 4 parts of force viz: (since it presseth equally on the points e & k ) it presseth on k with 2 parts of force & with the other 2 at e on the body aem so that aem presseth with 2 parts of force, viz: with one on the point { n }{ m } with the other on the point a ; Soe that the body hath 7 parts of pression upon the point n , 4 at h , 2 at k , & one at m , & since the pressure of all the point h k & m is directly towards { n } n will be pressed by it all. but the Globe causeth but one part of pression upon a . Now if these bodys fh , ek , aem , understood continually to diminish & come nearer to the line ad n the pressure of the body g upon a & n will still bee the same that is as 1 is to 7 , & so is the line dn to da . By the same reason it may be generally pronounced pressure of the body g upon to the pressure of it upon a
35 Or if the bodys a & n bee supposed united by the line ( and ) & another body moving towards them hit perpendicularly upon the line an at d ; as dn to ad so is the pressure of g upon { a } to its pressure upon n , so is the motion in to the motion in which is generated in them by those pressures of g , that is which they received from g , at the moment of reflection, & which they might continually injoy as in fig 6t.[111] did not their union by the line adn hinder
By the same reason if g reflect {nor} twixt the bodys, then pression of towards to the pression of a towards motion of n to { } motion of a to r .
Note that {illeg} & n are taken for the centers of motion in a & n . & adn for {illeg}
[112]
[113] 36 If the a & n doe rest, but soe that the body moveing perpendicularly to qp to them & refleting on the line qp (which is supported by but not fastened to the bodys a & n & ought now to be conceived a line onely.) doth move them by communicating its whole motion to them which it selfe looseth, Tis required what motion a & n shall receive from g . Suppose that in so much time as g moveth to before reflection in so much time it moveth from d to e after reflection & in so much time the bodys a & n move the one to r the other to s ; & that then the point of reflection is moved to . Then naming the given quantitys . . . . . the whole motion of & to & call , that is , or if , (then w is the center of the bodys motion ) ) & if , then is a line described by their center of motion Then is ( ) .[114] Now, as the motion of a to the motion of n (proposition 34) so is to ; Therefore (axiom 113) as the velocity of to the velocity of . that is . but ;that is ; or . & . . . therefore, . & . Also (by axiom 9th) . Therefore . Now since g hath soe much motion before reflection as all three bodys have afterward, therefore (axiom 113) ; Or, . That is . Or, . Or, calling ; then . Soe that by this Equation the point l twixt the bodys r & s being then their center of motion may bee always found. Note that the lines qr & ps must be described by the centers of motion of 2 bodys on divers sides of the point d that is ar by center of motion of the body or , & ps by the center of or
37 Now when a & n or ad & dn are united together (as in the 2d fig) they cannot seperate the one from the other, & therefore since (when they are not equivelox) rs is longer than pq , the one cannot be at s when the other is at r , but they will check the one the others motion soe as their centers of motion shall not describe streight lines (as or ) but crooked ones (as perhaps Trochoides as qmk , pht). yet the common center of their motion w or l shall retaine both the same determinacon & velocity that it would did the bodys move parallell to them selves or were they not united (by axiom {7}{17}). Soe that if the conjoyned bodys (fig 2d) move to m & h in the same time that they would have moved to r & s were they their center of motion when they are at m & h is {the} same that it would be wer they at {illeg} & therefore may be found by the {illeg} rule, viz; the {veloci}ty of the point l ; to the velocity of the body {illeg} befor{e}{illeg}{r}eflection. Vide
[1] {Se}{p}t 1664.
[2] 
[3] 
[4] 
[5] 
[6] 
[7] 
[8] 
[9] 
[10] 
[11] 
[12] 
[13] 
[14] 
[15] 
[16] 
[17] 
[18] 
[19] 
[20] 
[21] 
[22] 
[23] 
[24] 
[25] 
[26] 
[30]
[31] {illeg}
[34] 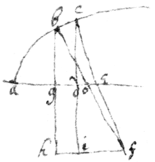
[35] 
[36]
[38] 
[39] .
[40] {illeg}
[41] {illeg}
[42] {illeg}.
[43] .
[44]
[45] {illeg} . {illeg}
[48] 
[49] 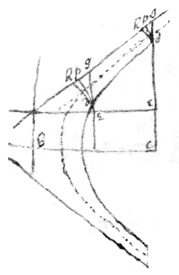
[50] 
[51] 
[52] 
[53] 
[54] 
[56] 
[57] 
[58] 
[59] . y
[60] 
[62] 
[63] 
[64]
Ian 20th 1664.
[65] 
[66] 
[67] Noe motion is lost in reflection. For the circular motion being made by continuall reflection would decay.
[68] 
[69] Def 3d
[70] {illeg}s Axiome 4th.
[71] 
[72] p Axiom 4th.
[74] r axiome 3d
[75] 
[76] 
[77] 
[78] The center of motions determinacon & velocity
[79] x axiom 14
[80] 
[82] 
[83] 
[84] 
[85] 
[86] 
[87] let this follow the 5t axiom
[88] 
[89] What force is required to beget or destroy equall velocity in unequall bodys
[91] What force Indeavor & Pression is
[92] What force or Motion is in equivelox bodys
[94] What motion in bodys
[95] 
A generall Theorem of the proportion of velocity & motion of given body moving ☞ through given spaces in given times.
[96] What force required to beget or destroy unequall celerity in equall bodys
[97] Of hindering and helping motion
[98] What celerity acquired or lost by equall forces in unequall bodys
[99] 
What velocity & motion gotten or lost by unequall forces in unequall bodys ☞ A Generall Theorem.
[101] 
[102] 
Two bodys being uniformely moved in the same plaine their center of motion which describe a streight line
[111] 
[112] 
[113] 
[114] 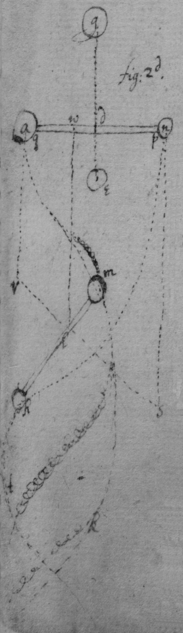




 .
.